Inhaltsverzeichnis
Die Statistik deiner Masterarbeit entscheidet darüber, ob deine Ergebnisse belastbar sind. Dieser Artikel zeigt dir, wie du den passenden Test findest, Voraussetzungen prüfst und Ergebnisse so berichtest, dass sie fachlichen Standards entsprechen.
Kurzantwort: Bei Gruppenvergleichen nutzt du t-Test (2 Gruppen) oder ANOVA (mehr als 2 Gruppen), bei Zusammenhängen Korrelation oder Regression. Prüfe vorher die Voraussetzungen und berichte mindestens Teststatistik, p-Wert und Effektstärke.
Statistik-Check in 3 Schritten: 1. Ziel bestimmen (Unterschied, Zusammenhang oder Vorhersage?), 2. Skalenniveau klären (AV nominal, ordinal oder metrisch?) und 3. Design prüfen (Unabhängige Gruppen oder Messwiederholung?).
Wähle dann den passenden Test (t-Test, ANOVA, Korrelation oder Regression), prüfe die Voraussetzungen (Normalverteilung, Varianzhomogenität) und berichte die Ergebnisse nach APA-Standard (Teststatistik, p-Wert, Effektstärke).
Welcher Test passt?
Die Frage nach dem richtigen statistischen Test ist oft der erste Stolperstein. Die Antwort ergibt sich aus drei Fragen: Was willst du herausfinden? Wie sind deine Daten skaliert? Wie ist dein Design aufgebaut? Die folgende Matrix hilft dir, deinen Kandidaten-Test direkt zu identifizieren.
Unterschied: 2 unabhängige Gruppen, AV metrisch
Test: t-Test (unabhängig) · Alternative bei Verletzung: Mann-Whitney-U
Unterschied: 2 abhängige Messungen (gleiche Personen), AV metrisch
Test: t-Test (abhängig/gepaart) · Alternative: Wilcoxon-Vorzeichen-Rang
Unterschied: mehr als 2 unabhängige Gruppen, AV metrisch
Test: Einfaktorielle ANOVA · Alternative: Kruskal-Wallis
Unterschied: mehr als 2 Messzeitpunkte (Messwiederholung), AV metrisch
Test: ANOVA mit Messwiederholung · Alternative: Friedman-Test
Zusammenhang: 2 metrische Variablen
Test: Pearson-Korrelation · Alternative: Spearman (ordinal oder Verletzung)
Vorhersage: AV metrisch, ein oder mehrere Prädiktoren
Test: Lineare Regression · Bei binärer AV: Logistische Regression
Zusammenhang: 2 kategoriale Variablen (Kreuztabelle)
Test: Chi-Quadrat-Test · Alternative: Fisher's Exact (kleine Zellhäufigkeiten)
Vorgaben können je nach Fach und Lehrstuhl variieren. Im Zweifel: Betreuung fragen.
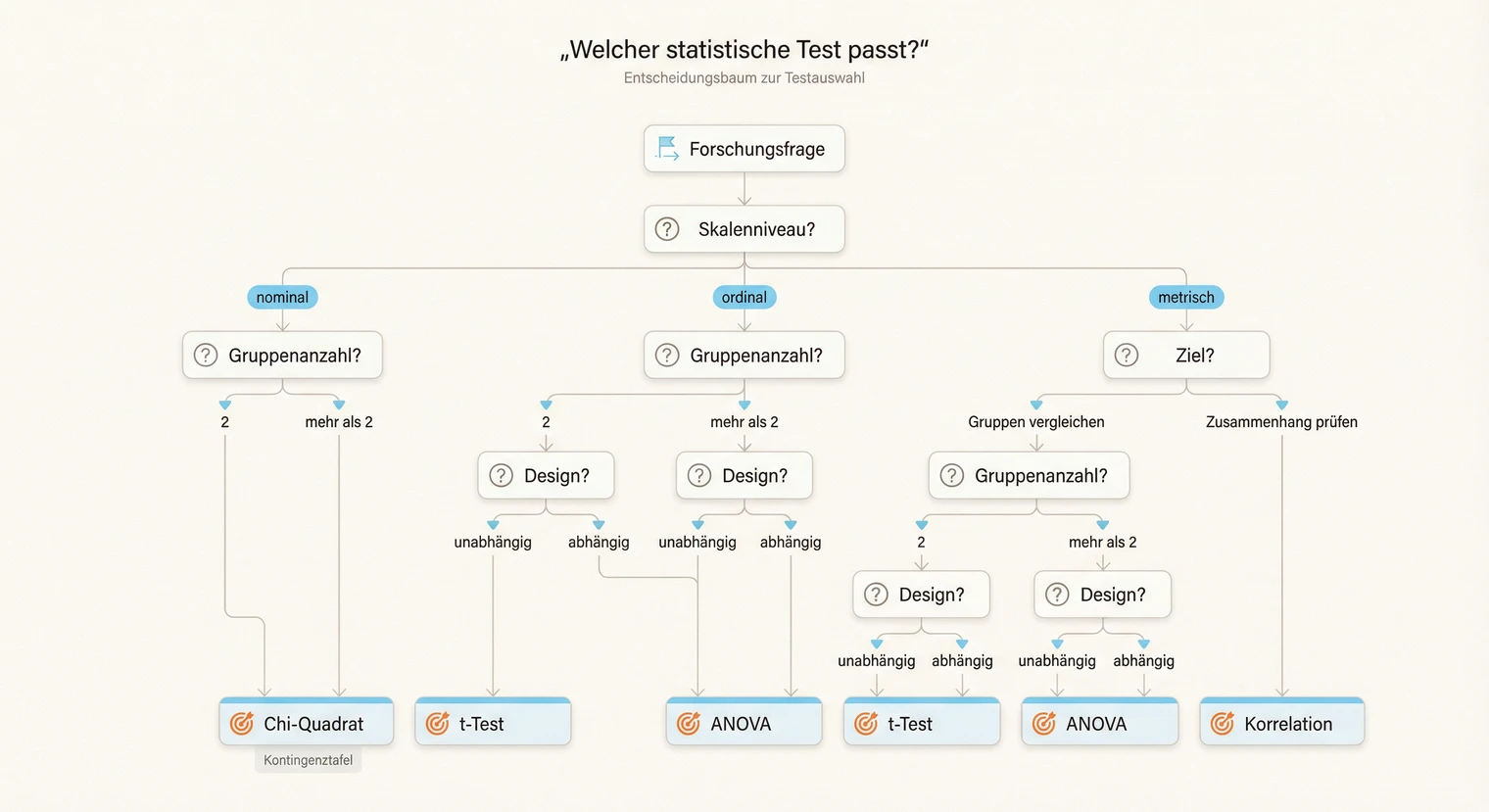
Bevor du dich für einen Test entscheidest, kläre deine Forschungsfrage präzise. Eine vage Frage führt zu unklarer Testwahl. Die Frage „Hat X einen Einfluss auf Y?" erfordert einen anderen Ansatz als „Unterscheiden sich Gruppe A und B in Y?".
Wenn dein Design über die Standardfälle hinausgeht, hier die wichtigsten Erweiterungen:
Mehrere Faktoren (z. B. Geschlecht × Trainingsmethode): Mehrfaktorielle ANOVA. Prüfe Interaktionseffekte.
Kovariate kontrollieren (z. B. Alter als Störvariable): ANCOVA oder multiple Regression. Kovariaten sollten theoretisch begründet sein und idealerweise zeitlich vor der UV liegen. Prüfe die Homogenität der Regressionssteigungen (Interaktion Kovariate × Gruppe). Wenn sich Gruppen bereits in der Kovariate unterscheiden, diskutiere das im Methodenteil (keine automatische „Wegkontrolle" von Gruppenunterschieden).
Messwiederholung + Gruppenfaktor: Mixed-Design ANOVA (between + within). Sphärizität für Within-Faktor prüfen.
Verschachtelte Daten (Klassen, Teams, Standorte): Mixed Models / Multilevel-Analyse. Standardverfahren unterschätzen sonst Standardfehler.
Mehrere abhängige Variablen gleichzeitig: MANOVA. Aber Vorsicht: Voraussetzungen strenger, Interpretation komplexer. Oft sind separate Analysen mit Korrektur praktikabler.
Bei diesen Designs: Besprich das Vorgehen frühzeitig mit deiner Betreuung oder der Methodenberatung deiner Uni.
Grundbegriffe der Statistik
Bevor du mit der Auswertung startest, solltest du die zentralen Begriffe sicher verstehen. Diese Grundlagen brauchst du für jeden statistischen Test.
Nominal: Kategorien ohne Rangfolge (Geschlecht, Studiengang). Nur Häufigkeiten zählbar.
Ordinal: Rangfolge, aber Abstände nicht gleich (Schulnoten, Zufriedenheit 1–5). Mediane vergleichbar.
Metrisch (Intervall/Ratio): Gleiche Abstände, Mittelwerte berechenbar (Alter, Einkommen, Temperatur). Voraussetzung für parametrische Tests.
M (Mittelwert): Durchschnitt aller Werte. Empfindlich gegenüber Ausreißern.
SD (Standardabweichung): Streuung um den Mittelwert. Je größer, desto heterogener die Daten.
Median: Wert in der Mitte der Verteilung. Robuster bei Ausreißern als der Mittelwert.
n: Stichprobengröße. Wichtig für die Power und Generalisierbarkeit.
Diese Grundbegriffe tauchen in jedem Ergebnisteil auf. Wenn du dir unsicher bist, halte ein Statistik-Lehrbuch griffbereit. Empfehlenswert sind Field (2018) für SPSS oder Bortz & Schuster für deutschsprachige Grundlagen.
Datenprobleme erkennen und lösen
Bevor du mit der eigentlichen Analyse startest, prüfe deine Daten auf typische Probleme. Ausreißer, fehlende Werte und falsche Kodierungen können statistische Ergebnisse verzerren oder komplett kippen. Eine sorgfältige Datenaufbereitung ist die Grundlage jeder belastbaren Auswertung.
Erkennen: Boxplots zeigen Werte außerhalb der Whisker (1,5-facher Interquartilsabstand). Histogramme machen extreme Werte sichtbar. Ein Alter von 999 oder negative Zeitwerte sind offensichtliche Eingabefehler.
Behandeln: Nicht automatisch löschen. Prüfe: Eingabefehler → korrigieren oder auf fehlend setzen. Echter Extremfall → Analyse mit und ohne Ausreißer durchführen, Ergebnisse vergleichen, Entscheidung begründen.
Dokumentieren: Halte im Methodenteil fest, wie du Ausreißer identifiziert und behandelt hast.
Anteil prüfen: Dokumentiere, wie viele Werte pro Variable fehlen. Als grobe Orientierung gilt: Unter 5 % und komplett zufällig verteilt (MCAR) ist oft unkritisch. Aber: Diese Schwelle ist keine feste Regel. Auch weniger Missings können problematisch sein, wenn sie systematisch auftreten (z. B. nur in einer Gruppe fehlen), sich auf zentrale Variablen konzentrieren oder das Missingness-Muster nicht zufällig ist (MNAR).
Strategien: Listwise Deletion (Fälle ausschließen) bei wenigen, zufälligen Missings. Bei mehr oder systematischen Missings: Multiple Imputation oder FIML. Pairwise Deletion vermeiden (führt zu unterschiedlichen n). Die Wahl hängt vom Missingness-Mechanismus, deinem Modell und den Fachkonventionen ab.
Im Methodenteil berichten: Anteil pro Variable, Muster (zufällig/systematisch?), gewählte Strategie mit Begründung, finale Stichprobengröße.
1. Invertierte Items umkodieren: Bei Skalen mit gegensätzlich formulierten Items (z. B. „Ich bin unzufrieden") musst du diese vor der Skalenbildung umkodieren. Formel: neuer Wert = (max + 1) – alter Wert. Bei 5er-Skala wird aus 4 dann 2.
2. Skalenwert bilden: Berechne den Mittelwert oder die Summe der Items pro Person. Bei Missings: Entscheide vorab, ob du den Skalenwert bei fehlenden Items trotzdem berechnest (z. B. wenn ≤ 20 % der Items fehlen) oder den Fall ausschließt.
3. Reliabilität berichten: Cronbachs α (oder McDonald's ω) misst die interne Konsistenz. Berichte α für jede Skala im Methodenteil: „Die interne Konsistenz der Skala war gut (α = .84)." Richtwerte: α ≥ .70 gilt oft als akzeptabel, aber das ist eine Konvention, keine feste Grenze. Bei kurzen Skalen (2–3 Items) sind niedrigere Werte erwartbar. Bei sehr hohem α (> .95) prüfe, ob Items redundant sind.
Konsistenz prüfen: Vor allem anderen: Sind alle Werte im erwarteten Bereich? Häufigkeitstabellen anschauen, bevor du weitermachst.
Für eine ausführliche Anleitung zur Datenaufbereitung und zum Umgang mit Missings schau dir den Artikel zur Datenanalyse in der Masterarbeit an.
Signifikanz und Effektstärke verstehen
Signifikanz und Effektstärke sind zwei verschiedene Konzepte, die oft verwechselt werden. Beide zusammen ergeben erst ein vollständiges Bild.

Der p-Wert gibt an, wie wahrscheinlich es ist, ein Ergebnis wie das beobachtete (oder extremer) zu erhalten, wenn die Nullhypothese wahr wäre. Er sagt nicht, wie wahrscheinlich deine Hypothese stimmt.
p < .05 als Konvention: In vielen Fächern gilt p < .05 als Schwelle für „statistisch signifikant". Diese Grenze ist eine weit verbreitete Konvention, keine naturgegebene Regel. In manchen Disziplinen (z. B. Teilchenphysik) gelten strengere Schwellen, in explorativen Studien werden teils liberalere Grenzen akzeptiert. Prüfe die Erwartungen deines Fachs und deiner Betreuung.
Signifikanz ≠ Relevanz: Ein signifikantes Ergebnis bei sehr großer Stichprobe kann praktisch unbedeutend sein. Ein nicht-signifikantes Ergebnis bei kleiner Stichprobe heißt nicht, dass kein Effekt existiert. Die Effektstärke zeigt, ob ein Unterschied auch praktisch bedeutsam ist.
Die Effektstärke zeigt die Größe eines Effekts unabhängig von der Stichprobe. Sie macht Ergebnisse vergleichbar.
Cohen's d (für Mittelwertvergleiche): |0.2| = klein, |0.5| = mittel, |0.8| = groß.
r (für Korrelationen): |.10| = klein, |.30| = mittel, |.50| = groß.
η² / η²p (für ANOVA): .01 = klein, .06 = mittel, .14 = groß.
Ein kleiner Effekt kann praktisch bedeutsam sein, wenn er viele Menschen betrifft. Ein großer Effekt kann trivial sein, wenn der Zusammenhang offensichtlich ist. Ordne Effektstärken immer im Kontext deines Forschungsfeldes ein.
Tests im Überblick
Hier findest du die wichtigsten statistischen Tests für Masterarbeiten mit ihren Einsatzgebieten und Voraussetzungen.
Einsatz: Vergleich der Mittelwerte zweier Gruppen.
Varianten: Unabhängig (zwei verschiedene Gruppen) oder abhängig (gleiche Personen, zwei Messzeitpunkte).
Voraussetzungen: Metrische AV, annähernde Normalverteilung, Varianzhomogenität (Levene-Test). Bei Varianzverletzung: Welch-t-Test.
Berichten: t(df) = X.XX, p = .XXX, d = X.XX
Einsatz: Vergleich der Mittelwerte von mehr als zwei Gruppen.
Varianten: Einfaktoriell (ein Faktor), mehrfaktoriell (mehrere Faktoren), mit Messwiederholung.
Voraussetzungen: Metrische AV, Normalverteilung, Varianzhomogenität. Bei Messwiederholung zusätzlich: Sphärizität (Mauchly-Test).
Berichten: F(df1, df2) = X.XX, p = .XXX, η²p = .XX. Bei signifikantem Haupteffekt: Post-hoc-Tests (Bonferroni, Tukey).
Einsatz: Zusammenhang zwischen zwei Variablen prüfen.
Pearson r: Für metrische, normalverteilte Variablen. Misst linearen Zusammenhang.
Spearman ρ: Für ordinale Daten oder bei Verletzung der Normalverteilung. Misst monotonen Zusammenhang.
Vorher prüfen: (1) Streudiagramm anschauen: Ist der Zusammenhang linear oder kurvenförmig? Pearson misst nur lineare Zusammenhänge – bei kurvenförmigen Beziehungen kann r trotz starkem Zusammenhang nahe 0 sein. (2) Ausreißer identifizieren: Einzelne Extremwerte können r stark verzerren. (3) Einschränkung der Varianz: Wird nur ein Teil des Wertebereichs erfasst, wird r unterschätzt.
Berichten: r = .XX, p = .XXX, 95% CI [.XX, .XX], n = XX
Einsatz: Vorhersage einer Variable durch eine oder mehrere andere.
Lineare Regression: AV metrisch. Logistische Regression: AV binär (ja/nein), berichte Odds Ratios (OR) mit CI.
Vorher prüfen (linear): (1) Linearität: Streudiagramm Residuen vs. Vorhersagewerte, kein Muster = okay. (2) Homoskedastizität: Residuenplot, Trichterform = Problem → robuste Standardfehler (alternativ: Transformation der AV oder andere Modellspezifikation, je nach Fach/Betreuung). (3) Normalverteilung der Residuen: Histogramm/Q-Q-Plot. (4) Multikollinearität: VIF < 5 (konservativ) oder < 10 (liberal), Schwellen variieren je nach Quelle. (5) Einflussreiche Fälle: Cook's D > 1 oder > 4/n (Faustregeln variieren), Analyse mit/ohne vergleichen.
Berichten: R² = .XX, F(df1, df2) = X.XX, p = .XXX. Pro Prädiktor: B, SE, β, t, p.
Einsatz: Zusammenhang zwischen zwei kategorialen Variablen (Kontingenz-/Kreuztabelle mit Häufigkeiten). Nicht zu verwechseln mit Gruppenvergleichen bei kategorialer AV.
Voraussetzung: Als Faustregel gilt: erwartete Häufigkeiten ≥ 5 in allen Zellen. Je nach Lehrbuch findest du auch ≥ 1 oder andere Varianten. Bei Verletzung: Fisher's Exact Test (2×2-Tabellen) oder Kategorien inhaltlich sinnvoll zusammenfassen. Bei größeren Tabellen auch Monte-Carlo-Simulation möglich.
Berichten: χ²(df) = X.XX, p = .XXX, Cramér's V = .XX
Für eine detaillierte Anleitung zur praktischen Durchführung mit Software schau dir den Artikel zur Datenanalyse in der Masterarbeit an.
Voraussetzungen prüfen
Jeder statistische Test hat Annahmen. Wenn diese verletzt sind, können die Ergebnisse irreführend sein. Hier sind die wichtigsten Checks.
Prüfen: Histogramm und Q-Q-Plot visuell beurteilen. Shapiro-Wilk-Test bei kleinen Stichproben (n < 50). Bei sehr großem n wird der Test fast immer signifikant, obwohl die Abweichung praktisch unbedeutend sein kann.
Zur „n > 30"-Faustregel: Oft heißt es, parametrische Tests seien ab n > 30 robust. Das ist eine Vereinfachung. Die Robustheit hängt vom konkreten Test, der Art der Verletzung (Schiefe vs. Ausreißer) und der Varianzstruktur ab. Schau dir deine Daten visuell an. Bei starker Schiefe, vielen Ausreißern oder sehr ungleichen Gruppengrößen können auch große Stichproben problematisch sein.
Wenn verletzt: Nicht-parametrische Alternative (Mann-Whitney, Kruskal-Wallis, Spearman) als Sensitivitätsanalyse durchführen und Entscheidung begründen.
Prüfen: Levene-Test. Signifikant (p < .05) bedeutet ungleiche Varianzen.
Wenn verletzt: Welch-t-Test statt klassischem t-Test. Bei ANOVA: Welch-ANOVA oder Games-Howell Post-hoc.
Was ist das? Die Varianzen der Differenzen zwischen allen Messpaaren sollten gleich sein.
Prüfen: Mauchly-Test. Signifikant = Verletzung.
Wenn verletzt: Greenhouse-Geisser-Korrektur (konservativ) oder Huynh-Feldt (liberal). Korrigierte Freiheitsgrade berichten.
Dokumentiere im Methodenteil, welche Voraussetzungen du geprüft hast und wie du mit Verletzungen umgegangen bist. Das zeigt methodische Sorgfalt und macht deine Ergebnisse nachvollziehbar.
Ergebnisse korrekt berichten
Statistisches Reporting folgt klaren Konventionen. In vielen Fächern gilt der APA-Stil als Standard. Hier sind Formulierungsbausteine, die du anpassen kannst.

t-Test (mit Zahlen, APA-Stil)
„Die Experimentalgruppe (M = 4.82, SD = 1.24, n = 45) erzielte signifikant höhere Werte in der Arbeitszufriedenheit als die Kontrollgruppe (M = 3.91, SD = 1.18, n = 43), t(86) = 3.56, p < .001, d = 0.76. Der Effekt ist nach Cohen als mittel bis groß einzustufen."
ANOVA (mit Zahlen, APA-Stil)
„Es zeigte sich ein signifikanter Haupteffekt des Faktors Trainingsmethode auf die Testleistung, F(2, 87) = 5.42, p = .006, η²p = .11. Post-hoc-Vergleiche (Bonferroni) ergaben, dass Methode A (M = 78.3) signifikant besser abschnitt als Methode C (M = 69.1, p = .004). Der Unterschied zwischen Methode A und B war nicht signifikant (p = .21)."
Korrelation (mit Zahlen, APA-Stil)
„Zwischen Arbeitsbelastung und Stresserleben bestand ein signifikant positiver Zusammenhang mittlerer Stärke, r = .42, p < .001, 95% CI [.26, .56], n = 112."
Regression (mit Zahlen, APA-Stil)
„Das Regressionsmodell war signifikant, F(3, 108) = 12.34, p < .001, R² = .26. Selbstwirksamkeit erwies sich als signifikanter Prädiktor der Leistungsmotivation (β = .38, t = 4.21, p < .001), während Alter (β = .08, p = .34) und Geschlecht (β = −.05, p = .56) keinen signifikanten Beitrag leisteten."
Musterformulierung: „[Beschreibung des Befunds in einem Satz]. [Teststatistik mit allen Kennwerten]. [Einordnung der Effektstärke in einem Satz]."
Beispiel (APA-Stil): „Die Intervention führte zu einer signifikanten Verbesserung der Lesekompetenz, t(58) = 2.89, p = .005, d = 0.75. Der Effekt entspricht nach Cohen einem mittleren bis großen Effekt."
Checkliste: Teststatistik (t, F, χ², r), Freiheitsgrade (df), p-Wert (exakt oder Schwelle), Effektstärke (d, η², r, V) sowie Stichprobengröße n.
Schreibweise: In deutschsprachigen Arbeiten ist neben dem APA-Stil (Punkt) auch das Komma üblich (d = 0,75). Bleibe im gesamten Text konsistent.
Wichtig: Im Ergebnisteil berichtest du, was du gefunden hast. Die Einordnung und Interpretation gehört in die Diskussion. Diese Trennung hilft, sachlich zu bleiben.
Typische Fehler vermeiden
Bei der statistischen Auswertung passieren einige Fehler immer wieder. Hier sind die häufigsten mit konkreten Gegenmaßnahmen.

1. Korrelation als Kausalität interpretieren: Ein Zusammenhang zeigt nicht, dass X Y verursacht. Formuliere vorsichtig („steht im Zusammenhang mit", nicht „bewirkt"). Kausale Aussagen nur bei experimentellem Design.
2. Nur p-Wert berichten: Signifikanz allein sagt wenig über praktische Relevanz. Ergänze die Effektstärke. Ein p < .001 bei kleinem Effekt kann praktisch unbedeutend sein.
3. Voraussetzungen ignorieren: Jeder Test hat Annahmen. Prüfe sie und dokumentiere das Vorgehen. Bei Verletzung: nicht-parametrische Alternative oder robuste Variante nutzen.
4. Multiple Tests ohne Korrektur: Viele Tests erhöhen die Wahrscheinlichkeit von Zufallsbefunden. Bei mehreren Vergleichen: Bonferroni- oder FDR-Korrektur anwenden.
5. Nicht-signifikant = kein Effekt: Ein p > .05 bedeutet nicht, dass kein Effekt existiert. Es könnte auch an zu kleiner Stichprobe liegen (geringe Power). Berichte stets Effektstärke und CI.
Ein weiterer häufiger Fehler: die Hypothesen erst nach der Analyse festlegen (HARKing). Definiere deine Hypothesen vorab und trenne konfirmatorische von explorativen Analysen. Das erhöht die Glaubwürdigkeit deiner Ergebnisse.
Nächste Schritte
Wenn du die statistische Grundlage verstanden hast, folgen die praktischen Schritte.
- Software einrichten: Prüfe, welche Statistik-Software an deinem Lehrstuhl üblich ist. SPSS ist in vielen sozialwissenschaftlichen Fächern Standard, R gewinnt an Bedeutung. Nutze Tutorials und die Methodenberatung deiner Uni für den Einstieg.
- Daten vorbereiten: Bevor du Tests durchführst, bereite deine Daten sorgfältig auf. Der Artikel zur Datenanalyse zeigt dir den kompletten Workflow von der Datenbereinigung bis zur Interpretation.
- Methodenteil schreiben: Dokumentiere dein statistisches Vorgehen nachvollziehbar. Welche Tests hast du gewählt und warum? Welche Voraussetzungen hast du geprüft? Die Forschungsmethoden deiner Arbeit sollten klar beschrieben sein.
- Frühzeitig mit Betreuung sprechen: Besprich dein statistisches Vorgehen mit deiner Betreuung, bevor du die Analyse durchführst. So vermeidest du, dass du am Ende feststellst, dass ein anderer Test erwartet wurde. Die meisten Lehrstühle haben Präferenzen für bestimmte Methoden oder Software.
Wenn die Statistik steht und deine Arbeit fertig geschrieben ist, folgt der letzte Schritt: Drucken und Binden. Deine Masterarbeit kannst du bei BachelorHero online konfigurieren.
Häufig gestellte Fragen
Wann nutze ich den Welch-t-Test statt des klassischen t-Tests?
Nutze den Welch-t-Test, wenn der Levene-Test auf ungleiche Varianzen hinweist (p < .05) oder wenn die Gruppengrößen stark unterschiedlich sind. Der Welch-Test ist robuster. SPSS zeigt beide Varianten; du entscheidest anhand des Levene-Tests. R nutzt Welch oft als Standard. Berichten: „Aufgrund ungleicher Varianzen wurde der Welch-t-Test durchgeführt, t(dfkorr) = X.XX, p = .XXX, d = X.XX."
Wie interpretiere ich ein Konfidenzintervall praktisch?
Würdest du die Studie sehr oft wiederholen, würden 95% der so berechneten 95%-Konfidenzintervalle den wahren Populationswert enthalten. Praktisch: Enthält das CI bei Mittelwertdifferenzen die Null, ist der Unterschied bei zweiseitigem Test nicht signifikant (α = .05). Breite CIs deuten auf hohe Unsicherheit hin (oft: kleine Stichprobe). Beispiel: „d = 0.65, 95% CI [0.22, 1.08]" – der Effekt ist signifikant positiv, weil das CI die Null nicht einschließt.
Wie groß muss meine Stichprobe sein?
Die nötige Stichprobengröße hängt von der erwarteten Effektgröße, dem gewünschten Power-Level (meist 80 %) und dem Alpha-Niveau ab. Nutze eine Power-Analyse mit G*Power oder vergleichbaren Tools. Faustregel: Je kleiner der erwartete Effekt, desto mehr Fälle brauchst du. Besprich das frühzeitig mit deiner Betreuung.
Welche Effektstärke passt zu welchem Test?
Cohen's d für t-Tests (Mittelwertvergleiche): klein = 0.2, mittel = 0.5, groß = 0.8. r für Korrelationen: klein = .10, mittel = .30, groß = .50. η²p (partielles Eta-Quadrat) für ANOVA: klein = .01, mittel = .06, groß = .14. Cramér's V für Chi-Quadrat: Die Cutoffs hängen von df ab (nach Cohen, grobe Orientierung: df = 1: .10/.30/.50; df = 2: .07/.21/.35) – im Zweifel Fachkonventionen oder Literatur heranziehen. Diese Werte sind Orientierung, keine festen Grenzen.
Was mache ich, wenn meine Daten nicht normalverteilt sind?
Prüfe zuerst, wie stark die Verletzung ist (Histogramm, Q-Q-Plot). Bei leichter Abweichung sind parametrische Tests oft robust, besonders bei größeren Stichproben. Bei starker Verletzung: nicht-parametrische Alternative nutzen (Mann-Whitney statt t-Test, Kruskal-Wallis statt ANOVA). Dokumentiere dein Vorgehen im Methodenteil.
Muss ich Statistik-Software wie SPSS nutzen?
In den meisten Fächern ja. SPSS ist weit verbreitet und hat eine intuitive Oberfläche. R ist kostenlos und flexibler, erfordert aber Programmierung. Excel reicht nur für deskriptive Statistik. Prüfe, welche Software an deinem Lehrstuhl üblich ist und wofür du Support bekommst.
 Interviewleitfaden erstellen
Interviewleitfaden erstellen  Forschungsstand der Masterarbeit
Forschungsstand der Masterarbeit  Interdisziplinäre Ansätze
Interdisziplinäre Ansätze